Constant Velocity Free Body Diagram

Miracle wherein objects appear to motion about their truthful positions in the sky

"Aberration of lite" redirects here. Not to be dislocated with Optical aberration.

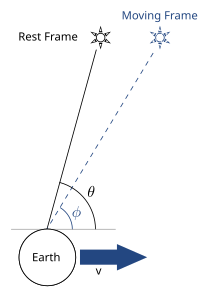
The credible position of a star viewed from the World depends on the Earth's velocity. The effect is typically much smaller than illustrated.

In astronomy, abnormality (also referred to every bit astronomical aberration, stellar abnormality, or velocity abnormality) is a phenomenon which produces an apparent move of angelic objects nigh their true positions, dependent on the velocity of the observer. It causes objects to appear to exist displaced towards the direction of motion of the observer compared to when the observer is stationary. The alter in angle is of the social club of v/c where c is the speed of light and v the velocity of the observer. In the case of "stellar" or "annual" aberration, the credible position of a star to an observer on Earth varies periodically over the class of a year as the World'south velocity changes as it revolves effectually the Sun, by a maximum angle of approximately xx arcseconds in right ascension or declination.

The term abnormality has historically been used to refer to a number of related phenomena concerning the propagation of calorie-free in moving bodies.^[1] Aberration is distinct from parallax, which is a change in the credible position of a relatively nearby object, as measured by a moving observer, relative to more afar objects that define a reference frame. The amount of parallax depends on the distance of the object from the observer, whereas aberration does not. Abnormality is also related to lite-time correction and relativistic beaming, although it is often considered separately from these furnishings.

Aberration is historically significant because of its role in the development of the theories of light, electromagnetism and, ultimately, the theory of special relativity. It was start observed in the late 1600s past astronomers searching for stellar parallax in order to confirm the heliocentric model of the Solar System. Even so, it was non understood at the time to be a different phenomenon.^[2] In 1727, James Bradley provided a classical explanation for it in terms of the finite speed of light relative to the motion of the Earth in its orbit effectually the Sun,^{[three] [4]} which he used to make i of the earliest measurements of the speed of light. Yet, Bradley'south theory was incompatible with 19th century theories of light, and abnormality became a major motivation for the aether elevate theories of Augustin Fresnel (in 1818) and K. One thousand. Stokes (in 1845), and for Hendrik Lorentz'south aether theory of electromagnetism in 1892. The abnormality of light, together with Lorentz's elaboration of Maxwell's electrodynamics, the moving magnet and conductor problem, the negative aether drift experiments, also as the Fizeau experiment, led Albert Einstein to develop the theory of special relativity in 1905, which presents a full general course of the equation for aberration in terms of such theory.^[five]

Explanation [edit]

Lite rays striking the earth in the Sun's rest frame compared to the same rays in the World's rest frame co-ordinate to special relativity. The issue is exaggerated for illustrative purposes.

Aberration may be explained as the deviation in bending of a beam of calorie-free in different inertial frames of reference. A common analogy is to consider the credible management of falling rain. If rain is falling vertically in the frame of reference of a person standing however, then to a person moving forwards the rain volition appear to get in at an angle, requiring the moving observer to tilt their umbrella frontward. The faster the observer moves, the more than tilt is needed.

The net effect is that light rays striking the moving observer from the sides in a stationary frame will come angled from ahead in the moving observer's frame. This event is sometimes chosen the "searchlight" or "headlight" effect.

In the example of annual abnormality of starlight, the direction of incoming starlight as seen in the Globe'southward moving frame is tilted relative to the angle observed in the Sun's frame. Since the direction of motion of the Earth changes during its orbit, the direction of this tilting changes during the class of the year, and causes the apparent position of the star to differ from its true position as measured in the inertial frame of the Sunday.

While classical reasoning gives intuition for abnormality, it leads to a number of physical paradoxes observable even at the classical level (see history). The theory of special relativity is required to correctly account for abnormality. The relativistic explanation is very like to the classical one however, and in both theories aberration may exist understood as a case of addition of velocities.

Classical caption [edit]

In the Sun's frame, consider a axle of calorie-free with velocity equal to the speed of light c, with 10 and y velocity components ${\displaystyle u_{x}}$ and ${\displaystyle u_{y}}$ , and thus at an angle θ such that ${\displaystyle \tan(\theta )=u_{y}/u_{x}}$ . If the Earth is moving at velocity ${\displaystyle v}$ in the 10 direction relative to the Lord's day, then by velocity addition the x component of the beam'due south velocity in the Earth'southward frame of reference is ${\displaystyle u_{10}'=u_{x}+five}$ , and the y velocity is unchanged, ${\displaystyle u_{y}'=u_{y}}$ . Thus the angle of the low-cal in the Earth'south frame in terms of the angle in the Sun's frame is

${\displaystyle \tan(\phi )={\frac {u_{y}'}{u_{ten}'}}={\frac {u_{y}}{u_{10}+five}}={\frac {\sin(\theta )}{five/c+\cos(\theta )}}}$

In the case of ${\displaystyle \theta =90^{\circ }}$ , this effect reduces to ${\displaystyle \tan(\theta -\phi )=five/c}$ , which in the limit ${\displaystyle v/c\ll one}$ may be approximated by ${\displaystyle \theta -\phi =v/c}$ .

Relativistic explanation [edit]

The reasoning in the relativistic instance is the same except that the relativistic velocity addition formulas must be used, which can be derived from Lorentz transformations between different frames of reference. These formulas are

${\displaystyle u_{x}'=(u_{x}+v)/(1+u_{x}v/c^{ii})}$

${\displaystyle u_{y}'=u_{y}/\gamma (1+u_{x}v/c^{2})}$

where ${\displaystyle \gamma =1/{\sqrt {1-v^{ii}/c^{2}}}}$ , giving the components of the lite beam in the Earth's frame in terms of the components in the Sun'due south frame. The bending of the beam in the Earth's frame is thus ^[vi]

${\displaystyle \tan(\phi )={\frac {u_{y}'}{u_{10}'}}={\frac {u_{y}}{\gamma (u_{x}+v)}}={\frac {\sin(\theta )}{\gamma (v/c+\cos(\theta ))}}}$

In the case of ${\displaystyle \theta =90^{\circ }}$ , this result reduces to ${\displaystyle \sin(\theta -\phi )=5/c}$ , and in the limit ${\displaystyle 5/c\ll 1}$ this may be approximated by ${\displaystyle \theta -\phi =v/c}$ . This relativistic derivation keeps the speed of light ${\displaystyle {\sqrt {u_{ten}^{2}+u_{y}^{2}}}=c}$ constant in all frames of reference, unlike the classical derivation above.

Relationship to light-fourth dimension correction and relativistic beaming [edit]

Aberration, lite-time correction, and relativistic beaming tin exist considered the same phenomenon depending on the frame of reference.

Aberration is related to two other phenomena, light-time correction, which is due to the move of an observed object during the time taken by its light to reach an observer, and relativistic beaming, which is an angling of the light emitted by a moving low-cal source. Information technology can be considered equivalent to them but in a different inertial frame of reference. In aberration, the observer is considered to exist moving relative to a (for the sake of simplicity^[7]) stationary light source, while in lite-time correction and relativistic beaming the light source is considered to exist moving relative to a stationary observer.

Consider the case of an observer and a light source moving relative to each other at constant velocity, with a light beam moving from the source to the observer. At the moment of emission, the beam in the observer's rest frame is tilted compared to the one in the source's rest frame, every bit understood through relativistic effulgent. During the time information technology takes the light axle to attain the observer the lite source moves in the observer's frame, and the 'true position' of the light source is displaced relative to the apparent position the observer sees, as explained by light-fourth dimension correction. Finally, the axle in the observer's frame at the moment of ascertainment is tilted compared to the beam in source'due south frame, which can be understood every bit an aberrational effect. Thus, a person in the lite source's frame would describe the credible tilting of the beam in terms of aberration, while a person in the observer's frame would describe it as a low-cal-fourth dimension outcome.

The human relationship betwixt these phenomena is only valid if the observer and source's frames are inertial frames. In exercise, because the Earth is not an inertial rest frame merely experiences centripetal acceleration towards the Sun, many aberrational furnishings such every bit almanac aberration on World cannot be considered light-time corrections. Yet, if the time between emission and detection of the lite is brusk compared to the orbital period of the Earth, the Earth may be approximated every bit an inertial frame and aberrational effects are equivalent to light-time corrections.

Types [edit]

The Astronomical Almanac describes several different types of aberration, arising from differing components of the World'south and observed object'due south move:

• Stellar aberration: "The apparent angular displacement of the observed position of a angelic trunk resulting from the movement of the observer. Stellar aberration is divided into diurnal, annual, and secular components."
  • Annual aberration: "The component of stellar aberration resulting from the movement of the Earth near the Dominicus."
  • Diurnal aberration: "The component of stellar aberration resulting from the observer'due south diurnal move virtually the center of the Earth due to the Earth's rotation."
  • Secular aberration: "The component of stellar aberration resulting from the substantially uniform and almost rectilinear motion of the entire solar system in space. Secular abnormality is ordinarily disregarded."
• Planetary aberration: "The apparent angular displacement of the observed position of a solar organization body from its instantaneous geocentric management as would exist seen by an observer at the geocenter. This displacement is caused by the abnormality of low-cal and light-time displacement."^[8]

Almanac aberration [edit]

Stars at the ecliptic poles appear to move in circles, stars exactly in the ecliptic plane move in lines, and stars at intermediate angles motility in ellipses. Shown here are the credible motions of stars with the ecliptic latitudes corresponding to these cases, and with ecliptic longitude of 270°.

The direction of abnormality of a star at the northern ecliptic pole differs at different times of the year

Annual abnormality is caused by the motion of an observer on World every bit the planet revolves around the Sunday. Due to orbital eccentricity, the orbital velocity ${\displaystyle v}$ of World (in the Sun's rest frame) varies periodically during the year as the planet traverses its elliptic orbit and consequently the aberration also varies periodically, typically causing stars to appear to move in small ellipses.

Approximating Earth's orbit as circular, the maximum displacement of a star due to annual aberration is known equally the abiding of aberration, conventionally represented by ${\displaystyle \kappa }$ . It may exist calculated using the relation ${\displaystyle \kappa =\theta -\phi \approx v/c}$ substituting the Earth'southward average speed in the Sun'southward frame for ${\displaystyle v}$ and the speed of light ${\displaystyle c}$ . Its accustomed value is xx.49552 arcseconds (sec) or 0.000099365 radians (rad) (at J2000).^[nine]

Assuming a round orbit, annual abnormality causes stars exactly on the ecliptic (the plane of Earth'due south orbit) to announced to move back and forth along a straight line, varying by ${\displaystyle \kappa }$ on either side of their position in the Sunday's frame. A star that is precisely at one of the ecliptic poles (at 90° from the ecliptic airplane) will appear to move in a circle of radius ${\displaystyle \kappa }$ about its true position, and stars at intermediate ecliptic latitudes volition appear to move along a small ellipse.

For illustration, consider a star at the northern ecliptic pole viewed by an observer at a indicate on the Chill Circle. Such an observer will encounter the star transit at the zenith, once every twenty-four hours (strictly speaking sidereal twenty-four hours). At the time of the March equinox, World'south orbit carries the observer in a southwards management, and the star's apparent declination is therefore displaced to the south by an angle of ${\displaystyle \kappa }$ . On the September equinox, the star's position is displaced to the n by an equal and opposite amount. On either solstice, the deportation in declination is 0. Conversely, the amount of displacement in right ascension is 0 on either equinox and at maximum on either solstice.

In actuality, Earth'southward orbit is slightly elliptic rather than circular, and its speed varies somewhat over the course of its orbit, which means the clarification higher up is only approximate. Aberration is more than accurately calculated using Earth'southward instantaneous velocity relative to the barycenter of the Solar System.^[9]

Notation that the deportation due to aberration is orthogonal to whatever displacement due to parallax. If parallax is detectable, the maximum displacement to the due south would occur in December, and the maximum displacement to the n in June. It is this evidently anomalous motion that so mystified early astronomers.

Solar annual aberration [edit]

A special case of annual aberration is the virtually constant deflection of the Sun from its position in the Sun's balance frame past ${\displaystyle \kappa }$ towards the west (as viewed from Earth), opposite to the apparent motion of the Lord's day along the ecliptic (which is from due west to east, as seen from Earth). The deflection thus makes the Sun appear to be behind (or retarded) from its remainder-frame position on the ecliptic by a position or angle ${\displaystyle \kappa }$ .

This deflection may equivalently exist described as a light-time effect due to motion of the Earth during the 8.3 minutes that it takes light to travel from the Sun to Earth. The relation with ${\displaystyle \kappa }$ is : [0.000099365 rad / 2 π rad] ten [365.25 d 10 24 h/d 10 sixty min/h] = 8.3167 min ≈ 8 min xix sec = 499 sec. This is possible since the transit time of sunlight is short relative to the orbital period of the Globe, so the Earth's frame may be approximated equally inertial. In the World's frame, the Sun moves, at a mean velocity v = 29.789 km/due south, past a altitude ${\displaystyle \Delta x=vt}$ ≈ 14,864.seven km in the time information technology takes lite to reach Earth, ${\displaystyle t=R/c}$ ≈ 499 sec for the orbit of mean radius ${\displaystyle R}$ = ane AU = 149,597,870.7 km. This gives an athwart correction ${\displaystyle \tan(\theta )\approx \theta =\Delta x/R}$ ≈ 0.000099364 rad = xx.49539 sec, which can exist solved to give ${\displaystyle \theta =v/c=\kappa }$ ≈ 0.000099365 rad = 20.49559 sec, very nearly the same as the aberrational correction (hither ${\displaystyle \kappa }$ is in radian and not in arcsecond).

Diurnal aberration [edit]

Diurnal abnormality is caused by the velocity of the observer on the surface of the rotating World. Information technology is therefore dependent not merely on the time of the observation, but also the latitude and longitude of the observer. Its outcome is much smaller than that of annual aberration, and is merely 0.32 arcseconds in the case of an observer at the Equator, where the rotational velocity is greatest.^[x]

Secular aberration [edit]

The secular component of aberration, caused by the motion of the Solar Arrangement in space, has been further subdivided into several components: aberration resulting from the motion of the solar organisation barycenter effectually the center of our Galaxy, aberration resulting from the motility of the Milky way relative to the Local Group, and aberration resulting from the movement of the Local Group relative to the cosmic microwave background.^{[11] : half dozen} Secular abnormality affects the apparent positions of stars and extragalactic objects. The large, constant part of secular aberration cannot be directly observed and "It has been standard exercise to absorb this large, nearly abiding issue into the reported"^{[12] : one} positions of stars.^[thirteen]

In about 200 million years, the Lord's day circles the galactic eye, whose measured location is near right ascension (α = 266.4°) and declination (δ = −29.0°).^{[12] : 2} The constant, unobservable, outcome of the solar arrangement's motion around the galactic center has been computed variously as 150^{[14] : 743} or 165^{[12] : 1} arcseconds. The other, observable, part is an acceleration toward the galactic centre of approximately 2.five × 10⁻¹⁰ thou/s², which yields a modify of aberration of about 5 µas/yr. Highly precise measurements extending over several years can discover this change in secular abnormality, often called the secular aberration drift or the acceleration of the Solar Arrangement, as a small apparent proper motion.^{[15] : ane [12] : 1}

Recently, highly precise astrometry of extragalactic objects using both Very Long Baseline Interferometry and the Gaia space observatory have successfully measured this small consequence.^[15] The outset VLBI measurement of the apparent motion, over a catamenia of 20 years, of 555 extragalactic objects towards the center of our milky way at equatorial coordinates of α = 263° and δ = −20° indicated a secular aberration migrate half-dozen.four ±i.five μas/yr.^{[xv] : 1} Subsequently determinations using a series of VLBI measurements extending over almost 40 years determined the secular abnormality drift to be v.83 ± 0.23 μas/yr in the direction α = 270.two ± ii.three° and δ = −20.ii° ± 3.six°.^{[11] : 7} Optical observations using only 33 months of Gaia satellite information of i.vi one thousand thousand extragalactic sources indicated an acceleration of the solar organisation of ii.32 ± 0.16 × 10⁻¹⁰ m/due southⁱⁱ and a corresponding secular abnormality drift of v.05 ± 0.35 µas/yr in the management of α = 269.1° ± 5.four°, δ = −31.6° ± 4.1°. It is expected that later Gaia data releases, incorporating nigh 66 and 120 months of data, volition reduce the random errors of these results by factors of 0.35 and 0.15.^{[xvi] [17] : 1,fourteen} The latest edition of the International Celestial Reference Frame (ICRF3) adopted a recommended galactocentric aberration constant of 5.8 µas/yr^{[12] : 5,vii} and recommended a correction for secular aberration to obtain the highest positional accuracy for times other than the reference epoch 2015.0.^{[11] : 17-19}

Planetary aberration [edit]

Planetary aberration is the combination of the aberration of calorie-free (due to Earth's velocity) and light-fourth dimension correction (due to the object's motion and altitude), as calculated in the balance frame of the Solar System. Both are determined at the instant when the moving object'south low-cal reaches the moving observer on Earth. It is so called because it is unremarkably applied to planets and other objects in the Solar System whose movement and distance are accurately known.

Discovery and starting time observations [edit]

The discovery of the aberration of light was totally unexpected, and information technology was simply by considerable perseverance and perspicacity that Bradley was able to explicate it in 1727. Information technology originated from attempts to observe whether stars possessed appreciable parallaxes.

Search for stellar parallax [edit]

The Copernican heliocentric theory of the Solar Organization had received confirmation by the observations of Galileo and Tycho Brahe and the mathematical investigations of Kepler and Newton.^[eighteen] As early as 1573, Thomas Digges had suggested that parallactic shifting of the stars should occur according to the heliocentric model, and consequently if stellar parallax could be observed information technology would help ostend this theory. Many observers claimed to take adamant such parallaxes, simply Tycho Brahe and Giovanni Battista Riccioli concluded that they existed merely in the minds of the observers, and were due to instrumental and personal errors. However, in 1680 Jean Picard, in his Voyage d'Uranibourg, stated, as a result of 10 years' observations, that Polaris, the Pole Star, exhibited variations in its position amounting to 40″ annually. Some astronomers endeavoured to explicate this past parallax, only these attempts failed because the motion differed from that which parallax would produce. John Flamsteed, from measurements made in 1689 and succeeding years with his mural quadrant, similarly concluded that the declination of Polaris was xl″ less in July than in September. Robert Hooke, in 1674, published his observations of γ Draconis, a star of magnitude 2^m which passes practically overhead at the breadth of London (hence its observations are largely free from the complex corrections due to atmospheric refraction), and concluded that this star was 23″ more northerly in July than in October.^[18]

James Bradley's observations [edit]

Consequently, when Bradley and Samuel Molyneux entered this sphere of research in 1725, in that location was nonetheless considerable doubt as to whether stellar parallaxes had been observed or not, and it was with the intention of definitely answering this question that they erected a large telescope at Molyneux's house at Kew.^[four] They decided to reinvestigate the motion of γ Draconis with a telescope constructed by George Graham (1675–1751), a celebrated instrument-maker. This was fixed to a vertical chimney stack in such manner every bit to permit a minor oscillation of the eyepiece, the corporeality of which (i.east. the deviation from the vertical) was regulated and measured by the introduction of a screw and a plumb line.^[18]

The musical instrument was set upward in November 1725, and observations on γ Draconis were made starting in December. The star was observed to move 40″ southwards between September and March, then reversed its class from March to September. ^[18] At the same time, 35 Camelopardalis, a star with a right rising virtually exactly opposite to that of γ Draconis, was nineteen" more northerly at the showtime of March than in September.^[nineteen] These results were completely unexpected and inexplicable by existing theories.

Early on hypotheses [edit]

Hypothetical observation of γ Draconis if its motility was acquired by parallax.

Hypothetical observation of γ Draconis and 35 Camelopardalis if their movements were acquired past nutation.

Bradley and Molyneux discussed several hypotheses in the hope of finding the solution. Since the credible move was patently caused neither by parallax nor observational errors, Bradley first hypothesized that information technology could exist due to oscillations in the orientation of the Earth's axis relative to the angelic sphere – a phenomenon known equally nutation. 35 Camelopardalis was seen to possess an apparent motion which could be consequent with nutation, but since its declination varied but one half as much as that of γ Draconis, it was obvious that nutation did non supply the respond^[20] (nonetheless, Bradley later went on to discover that the Earth does indeed nutate).^[21] He also investigated the possibility that the motion was due to an irregular distribution of the Earth's atmosphere, thus involving abnormal variations in the refractive index, but over again obtained negative results.^[20]

On Baronial nineteen, 1727, Bradley embarked upon a farther serial of observations using a telescope of his own erected at the Rectory, Wanstead. This instrument had the advantage of a larger field of view and he was able to obtain precise positions of a large number of stars over the course of well-nigh xx years. During his first two years at Wanstead, he established the existence of the phenomenon of abnormality beyond all doubtfulness, and this also enabled him to formulate a set of rules that would allow the calculation of the consequence on whatsoever given star at a specified appointment.

Evolution of the theory of abnormality [edit]

Bradley eventually developed his explanation of abnormality in virtually September 1728 and this theory was presented to the Royal Society in mid January the following yr. One well-known story was that he saw the change of direction of a wind vane on a boat on the Thames, caused non by an amending of the air current itself, but by a change of form of the boat relative to the wind management.^[21] However, in that location is no tape of this incident in Bradley'due south own business relationship of the discovery, and information technology may therefore be counterfeit.

The following table shows the magnitude of departure from true declination for γ Draconis and the management, on the planes of the solstitial colure and ecliptic prime number meridian, of the tangent of the velocity of the Earth in its orbit for each of the four months where the extremes are constitute, as well as expected deviation from true ecliptic longitude if Bradley had measured its deviation from right ascension:

Month	Direction of tangential velocity of Earth on the plane of the solstitial colure	Departure from truthful declination of γ Draconis	Management of tangential velocity of Earth on the plane of the ecliptic prime meridian	Expected deviation from true ecliptic longitude of γ Draconis
December	zero	none	← (moving toward perihelion at fast velocity)	decrease of more than twenty.ii"
March	← (moving toward aphelion)	19.5" southward	null	none
June	zero	none	→ (moving toward aphelion at slow velocity)	increase of less than twenty.ii"
September	→ (moving toward perihelion)	nineteen.five" due north	zero	none

Bradley proposed that the aberration of light non merely affected declination, only right ascension as well, and so that a star in the pole of the ecliptic would draw a little ellipse with a bore of about 40", merely for simplicity, he assumed information technology to be a circle. Since he only observed the departure in declination, and not in correct rising, his calculations for the maximum deviation of a star in the pole of the ecliptic are for its declination only, which will coincide with the diameter of the petty circle described by such star. For viii different stars, his calculations are every bit follows:

Star	Annual Variation (")	Maximum divergence in declination of a star in the pole of the ecliptic (")
γ Draconis	39	40.4
β Draconis	39	twoscore.2
η Ursa Maj.	36	40.4
α Cass.	34	forty.8
τ Persei	25	41.0
α Persei	23	xl.2
35 Camel.	xix	twoscore.2
Capella	sixteen	40.0
Hateful		40.four

Based on these calculations, Bradley was able to gauge the constant of abnormality at 20.two", which is equal to 0.00009793 radians, and with this was able to estimate the speed of low-cal at 183,300 miles (295,000 km) per second.^[22] By projecting the little circle for a star in the pole of the ecliptic, he could simplify the calculation of the relationship betwixt the speed of light and the speed of the World's annual motion in its orbit as follows:

${\displaystyle \cos \left({\frac {1}{ii}}\pi -0.00009793\right)=\sin(0.00009793)={\frac {v}{c}}}$

Thus, the speed of light to the speed of the Earth's annual motion in its orbit is x,210 to i, from whence it would follow, that light moves, or is propagated as far as from the Sun to the Earth in eight minutes 12 seconds.^[23]

The discovery and elucidation of aberration is at present regarded as a case of the awarding of scientific method, in which observations are fabricated to test a theory, but unexpected results are sometimes obtained that in turn lead to new discoveries. Part of the original motivation of the search for stellar parallax was to test the Copernican theory that the Earth revolves around the Sun. The modify of annual aberration in the class of the year demonstrates both the almanac motion of the Earth around the Dominicus and the relative movement of the World and the stars.

Retrodiction on Descartes' lightspeed statement [edit]

In the prior century, René Descartes argued that if low-cal were non instantaneous, and so shadows of moving objects would lag; and if propagation times over terrestrial distances were appreciable, and then during a lunar eclipse the Sun, World, and Moon would be out of alignment by hours' move, contrary to ascertainment. Huygens commented that, on Rømer'southward lightspeed information (yielding an earth-moon circular-trip time of simply seconds), the lag angle would be imperceptible. What they both overlooked^[24] is that aberration (as understood only later) would exactly annul the lag even if big, leaving this eclipse method completely insensitive to lite speed. (Otherwise, shadow-lag methods could be made to sense absolute translational movement, contrary to a basic principle of relativity.)

Historical theories of aberration [edit]

The phenomenon of abnormality became a driving force for many concrete theories during the 200 years between its observation and the caption past Albert Einstein.

The first classical explanation was provided in 1729, by James Bradley as described to a higher place, who attributed it to the finite speed of light and the motion of Globe in its orbit around the Sun.^{[iii] [iv]} Withal, this explanation proved inaccurate one time the wave nature of light was amend understood, and correcting it became a major goal of the 19th century theories of luminiferous aether. Augustin-Jean Fresnel proposed a correction due to the motion of a medium (the aether) through which light propagated, known equally "partial aether drag". He proposed that objects partially drag the aether along with them as they move, and this became the accustomed explanation for aberration for some time. George Stokes proposed a like theory, explaining that aberration occurs due to the flow of aether induced by the motion of the Earth. Accumulated prove against these explanations, combined with new understanding of the electromagnetic nature of light, led Hendrik Lorentz to develop an electron theory which featured an immobile aether, and he explained that objects contract in length as they move through the aether. Motivated past these previous theories, Albert Einstein and so developed the theory of special relativity in 1905, which provides the modernistic account of abnormality.

Bradley's classical explanation [edit]

Figure 2: As low-cal propagates down the telescope, the telescope moves requiring a tilt to the telescope that depends on the speed of light. The credible angle of the star φ differs from its true angle θ.

Bradley conceived of an explanation in terms of a corpuscular theory of light in which lite is made of particles.^[1] His classical caption appeals to the motion of the globe relative to a beam of calorie-free-particles moving at a finite velocity, and is developed in the Sun's frame of reference, dissimilar the classical derivation given above.

Consider the instance where a distant star is motionless relative to the Sun, and the star is extremely far abroad, so that parallax may exist ignored. In the rest frame of the Sun, this means light from the star travels in parallel paths to the World observer, and arrives at the same angle regardless of where the Globe is in its orbit. Suppose the star is observed on Earth with a telescope, idealized as a narrow tube. The light enters the tube from the star at angle ${\displaystyle \theta }$ and travels at speed ${\displaystyle c}$ taking a time ${\displaystyle h/c}$ to reach the lesser of the tube, where it is detected. Suppose observations are made from Earth, which is moving with a speed ${\displaystyle v}$ . During the transit of the lite, the tube moves a distance ${\displaystyle vh/c}$ . Consequently, for the particles of light to accomplish the lesser of the tube, the tube must be inclined at an angle ${\displaystyle \phi }$ dissimilar from ${\displaystyle \theta }$ , resulting in an credible position of the star at bending ${\displaystyle \phi }$ . As the Earth proceeds in its orbit it changes direction, and then ${\displaystyle \phi }$ changes with the fourth dimension of year the ascertainment is made. The credible angle and true angle are related using trigonometry as:

${\displaystyle \tan(\phi )={\frac {h\sin(\theta )}{hv/c+h\cos(\theta )}}={\frac {\sin(\theta )}{v/c+\cos(\theta )}}}$ .

In the example of ${\displaystyle \theta =90^{\circ }}$ , this gives ${\displaystyle \tan(\theta -\phi )=v/c}$ . While this is dissimilar from the more accurate relativistic outcome described above, in the limit of small angle and depression velocity they are approximately the aforementioned, inside the error of the measurements of Bradley's mean solar day. These results allowed Bradley to make one of the primeval measurements of the speed of low-cal.^{[23] [25]}

Luminiferous aether [edit]

Young reasoned that aberration could only exist explained if the aether were immobile in the frame of the Sun. On the left, stellar aberration occurs if an immobile aether is causeless, showing that the telescope must be tilted. On the right, the aberration disappears if the aether moves with the telescope, and the telescope does non need to exist tilted.

In the early on nineteenth century the moving ridge theory of light was being rediscovered, and in 1804 Thomas Immature adjusted Bradley'southward caption for corpuscular low-cal to wavelike light traveling through a medium known every bit the luminiferous aether. His reasoning was the same as Bradley's, only it required that this medium be immobile in the Sun's reference frame and must pass through the earth unaffected, otherwise the medium (and therefore the light) would move along with the earth and no aberration would be observed. ^[26] He wrote:

Upon consideration of the phenomena of the aberration of the stars I am tending to believe that the luminiferous aether pervades the substance of all cloth bodies with niggling or no resistance, as freely possibly as the wind passes through a grove of trees.

—Thomas Immature, 1804^[1]

Nonetheless, it before long became articulate Young'south theory could non account for aberration when materials with a non-vacuum index of refraction were present. An important example is of a telescope filled with water. The velocity of the light in such a telescope will be slower than in vacuum, and is given by ${\displaystyle c/n}$ rather than ${\displaystyle c}$ where ${\displaystyle due north}$ is the index of refraction of the water. Thus, by Bradley and Young's reasoning the aberration angle is given by

${\displaystyle \tan(\phi )={\frac {\sin(\theta )}{v/(c/north)+\cos(\theta )}}}$ .

which predicts a medium-dependent angle of aberration. When refraction at the telescope'due south objective is taken into business relationship this result deviates fifty-fifty more from the vacuum result. In 1810 François Arago performed a like experiment and found that the aberration was unaffected by the medium in the telescope, providing solid evidence against Young'south theory. This experiment was subsequently verified by many others in the post-obit decades, nigh accurately by Airy in 1871, with the same issue.^[26]

Aether drag models [edit]

Fresnel'southward aether drag [edit]

In 1818, Augustin Fresnel developed a modified explanation to business relationship for the h2o telescope and for other aberration phenomena. He explained that the aether is generally at rest in the Sun's frame of reference, merely objects partially drag the aether along with them as they move. That is, the aether in an object of index of refraction ${\displaystyle n}$ moving at velocity ${\displaystyle v}$ is partially dragged with a velocity ${\displaystyle (1-ane/n^{2})v}$ bringing the light along with it. This factor is known as "Fresnel's dragging coefficient". This dragging result, forth with refraction at the telescope'south objective, compensates for the slower speed of lite in the h2o telescope in Bradley'due south explanation.^[a] With this modification Fresnel obtained Bradley'southward vacuum result even for non-vacuum telescopes, and was also able to predict many other phenomena related to the propagation of low-cal in moving bodies. Fresnel's dragging coefficient became the dominant caption of aberration for the next decades.

Conceptual analogy of Stokes' aether drag theory. In the rest frame of the Sun the Earth moves to the right through the aether, in which it induces a local current. A ray of light (in red) coming from the vertical becomes dragged and tilted due to the menstruation of aether.

Stokes' aether drag [edit]

However, the fact that calorie-free is polarized (discovered past Fresnel himself) led scientists such as Cauchy and Greenish to believe that the aether was a totally immobile rubberband solid as opposed to Fresnel's fluid aether. In that location was thus renewed need for an explanation of aberration consistent both with Fresnel's predictions (and Arago's observations) besides as polarization.

In 1845, Stokes proposed a 'putty-similar' aether which acts as a liquid on large scales but as a solid on small-scale scales, thus supporting both the transverse vibrations required for polarized light and the aether flow required to explicate aberration. Making only the assumptions that the fluid is irrotational and that the boundary conditions of the flow are such that the aether has nil velocity far from the Earth, merely moves at the Earth's velocity at its surface and within it, he was able to completely account for aberration.^[b] The velocity of the aether exterior of the Globe would subtract as a part of altitude from the Earth so low-cal rays from stars would be progressively dragged as they approached the surface of the World. The World's motion would exist unaffected by the aether due to D'Alembert's paradox.

Both Fresnel and Stokes' theories were pop. However, the question of abnormality was put aside during much of the second one-half of the 19th century as focus of enquiry turned to the electromagnetic backdrop of aether.

Lorentz' length wrinkle [edit]

In the 1880s once electromagnetism was better understood, interest turned again to the problem of aberration. By this time flaws were known to both Fresnel's and Stokes' theories. Fresnel'due south theory required that the relative velocity of aether and thing to be dissimilar for lite of different colors, and information technology was shown that the purlieus conditions Stokes had assumed in his theory were inconsistent with his supposition of irrotational menses.^{[1] [26] [27]} At the same time, the modern theories of electromagnetic aether could non business relationship for aberration at all. Many scientists such equally Maxwell, Heaviside and Hertz unsuccessfully attempted to solve these problems by incorporating either Fresnel or Stokes' theories into Maxwell'due south new electromagnetic laws.

Hendrik Lorentz spent considerable effort along these lines. Later working on this problem for a decade, the issues with Stokes' theory caused him to abandon it and to follow Fresnel's suggestion of a (generally) stationary aether (1892, 1895). However, in Lorentz'due south model the aether was completely immobile, like the electromagnetic aethers of Cauchy, Green and Maxwell and dissimilar Fresnel's aether. He obtained Fresnel's dragging coefficient from modifications of Maxwell's electromagnetic theory, including a modification of the time coordinates in moving frames ("local time"). In lodge to explain the Michelson–Morley experiment (1887), which plainly contradicted both Fresnel'southward and Lorentz's immobile aether theories, and apparently confirmed Stokes' complete aether drag, Lorentz theorized (1892) that objects undergo "length wrinkle" past a factor of ${\displaystyle {\sqrt {1-v^{ii}/c^{ii}}}}$ in the direction of their motion through the aether. In this way, abnormality (and all related optical phenomena) tin be accounted for in the context of an immobile aether. Lorentz' theory became the basis for much research in the adjacent decade, and beyond. Its predictions for aberration are identical to those of the relativistic theory.^{[26] [28]}

Special relativity [edit]

Lorentz' theory matched experiment well, but it was complicated and made many unsubstantiated physical assumptions most the microscopic nature of electromagnetic media. In his 1905 theory of special relativity, Albert Einstein reinterpreted the results of Lorentz' theory in a much simpler and more than natural conceptual framework which disposed of the thought of an aether. His derivation is given above, and is at present the accepted caption. Robert South. Shankland reported some conversations with Einstein, in which Einstein emphasized the importance of abnormality:^[29]

He continued to say the experimental results which had influenced him most were the observations of stellar aberration and Fizeau's measurements on the speed of light in moving water. "They were plenty," he said.

Other important motivations for Einstein'southward development of relativity were the moving magnet and usher problem and (indirectly) the negative aether drift experiments, already mentioned by him in the introduction of his beginning relativity paper. Einstein wrote in a annotation in 1952:^[5]

My own thought was more indirectly influenced by the famous Michelson-Morley experiment. I learned of it through Lorentz' path breaking investigation on the electrodynamics of moving bodies (1895), of which I knew before the establishment of the special theory of relativity. Lorentz' bones supposition of a resting ether did not seem directly convincing to me, since it led to an [struck out: to me artificial appearing] interpretation of the Michelson-Morley experiment, which [struck out: did not convince me] seemed unnatural to me. My direct path to the sp. th. rel. was mainly determined by the conviction that the electromotive strength induced in a conductor moving in a magnetic field is null other than an electric field. Only the upshot of Fizeau's experiment and the phenomenon of abnormality also guided me.

While Einstein'south result is the same equally Bradley's original equation except for an extra factor of ${\displaystyle \gamma }$ , Bradley's result does non just give the classical limit of the relativistic instance, in the sense that it gives incorrect predictions even at low relative velocities. Bradley's caption cannot account for situations such equally the water telescope, nor for many other optical furnishings (such as interference) that might occur within the telescope. This is considering in the Earth'southward frame it predicts that the direction of propagation of the light beam in the telescope is non normal to the wavefronts of the axle, in contradiction with Maxwell'southward theory of electromagnetism. Information technology also does not preserve the speed of light c between frames. However, Bradley did correctly infer that the effect was due to relative velocities.

See also [edit]

• Apparent place
• Stellar parallax
• Astronomical nutation
• Proper motion
• Timeline of electromagnetism and classical optics
• Stellar aberration (derivation from Lorentz transformation)
• Relativistic aberration

Notes [edit]

1. ^ More in detail, Fresnel explains that the incoming calorie-free of angle ${\displaystyle \theta }$ is beginning refracted at the end of the telescope, to a new angle ${\displaystyle \psi }$ within the telescope. This may exist deemed for by Snell'due south law, giving ${\displaystyle \sin(\theta -\phi )=northward\sin(\psi -\phi )}$ . And so elevate must be accounted for. Without drag, the x and y components of the light in the telescope are ${\displaystyle (c/n)\sin(\psi )}$ and ${\displaystyle (c/n)\cos(\psi )}$ , but drag modifies the x component to ${\displaystyle (c/n)\cos(\psi )-(1-1/n^{2})v}$ if the Earth moves with velocity ${\displaystyle v}$ . If ${\displaystyle \blastoff }$ is angle and ${\displaystyle v_{l}}$ is the velocity of the calorie-free with these velocity components, then by Bradley'south reasoning ${\displaystyle \tan(\phi )={\frac {h\sin(\alpha )}{vt+h\cos(\alpha )}}}$ where ${\displaystyle h}$ is the modified path length through the water and t is the time it takes the light to travel the distance h, ${\displaystyle t=h/v_{l}}$ . Upon solving these equations for ${\displaystyle \phi }$ in terms of ${\displaystyle \theta }$ one obtains Bradley's vacuum consequence.
2. ^

   

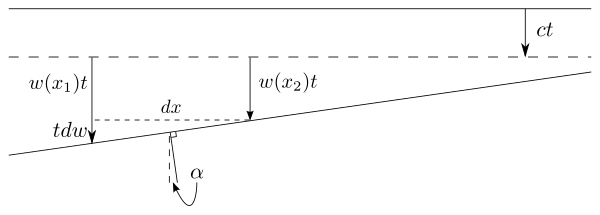
   Stokes' derivation may be summarized as follows: Consider a wavefront moving in the downwardly z direction. Say the aether has velocity field ${\displaystyle u,v,w}$ as a function of ${\displaystyle 10,y,z}$ . Now, motion of the aether in the x and y directions does not bear on the wavefront, but the motion in the z direction advances it (in addition to the amount it advances at speed c). If the z velocity of the aether varies over space, for case if it is slower for college x equally shown in the figure, and so the wavefront becomes angled, by an angle ${\displaystyle \tan(\blastoff )=tdw/dx}$ . Now, say in time t the wavefront has moved by a span ${\displaystyle dz\approx ct}$ (bold the speed of the aether is negligible compared to the speed of light). Then for each distance ${\displaystyle dz}$ the ray descends, it is aptitude by an bending ${\displaystyle \alpha \approx (dw/dx)(dz/c)}$ , and and so the total angle by which it has changed after travelling through the entire fluid is

   ${\displaystyle \alpha \approx {\frac {ane}{c}}\int {\frac {\partial w}{\partial x}}dz}$

   If the fluid is irrotational information technology will satisfy the Cauchy–Riemann equations, one of which is

   ${\displaystyle {\frac {\partial w}{\fractional ten}}={\frac {\partial u}{\partial z}}}$ .

   Inserting this into the previous consequence gives an abnormality angle ${\displaystyle \alpha =(u_{2}-u_{1})/c}$ where the ${\displaystyle u}$ s represent the 10 component of the aether'due south velocity at the start and finish of the ray. Far from the earth the aether has zero velocity, and so ${\displaystyle u_{2}=0}$ and at the surface of the globe it has the globe'south velocity ${\displaystyle five}$ . Thus we finally go

   ${\displaystyle \alpha \approx {\frac {v}{c}}}$

   which is the known abnormality outcome.

References [edit]

1. ^ ^{a b c d} Schaffner, Kenneth F. (1972), Nineteenth-century aether theories, Oxford: Pergamon Press, pp. 99–117 und 255–273, ISBN0-08-015674-six
2. ^ Williams, K. Due east. W. (1979). "Flamsteed's Declared Measurement of Almanac Parallax for the Pole Star". Journal for the History of Astronomy. 10 (ii): 102–116. Bibcode:1979JHA....ten..102W. doi:x.1177/002182867901000203. S2CID 118565124.
3. ^ ^{a b} Bradley, James (1727–1728). "A Letter of the alphabet from the Reverend Mr. James Bradley Savilian Professor of Astronomy at Oxford, and F.R.S. to MdEdmond Halley Astronom. Reg. &c. Giving an Business relationship of a New Discovered Motion of the Gear up'd Stars". Phil. Trans. R. Soc. 35 (406): 637–661. Bibcode:1727RSPT...35..637B. doi:10.1098/rstl.1727.0064.
4. ^ ^{a b c} Hirschfeld, Alan (2001). Parallax:The Race to Measure the Cosmos. New York, New York: Henry Holt. ISBN0-8050-7133-4.
5. ^ ^{a b} Norton, John D. (2004), "Einstein'due south Investigations of Galilean Covariant Electrodynamics prior to 1905", Annal for History of Verbal Sciences, 59 (one): 45–105, Bibcode:2004AHES...59...45N, doi:ten.1007/s00407-004-0085-half-dozen, S2CID 17459755, archived from the original on 2009-01-11
6. ^ Richard A. Mould (2001). Basic Relativity (2nd ed.). Springer. p. 8. ISBN0-387-95210-ane.
7. ^ In fact, the light source doesn't demand to be stationary, consider for example eclipsing binary stars: they are rotating with high speed —and ever changing and dissimilar velocity vectors— around each other, simply they appear every bit ane spot all the time.
8. ^ U.S. Nautical Annual Office (21 March 2014), "Glossary", Astronomical Almanac for the Twelvemonth 2015 and Its Companion, The Astronomical Almanac Online, Washington, DC: U.Due south. Authorities Press Office (published 2014), p. M1, ISBN9780707741499
9. ^ ^{a b} Kovalevsky, Jean & Seidelmann, P. Kenneth (2004). Fundamentals of Astrometry. Cambridge: Cambridge University Press. ISBN0-521-64216-seven.
10. ^ Newcomb, Simon (1960). A Compendium of Spherical Astronomy. Macmillan, 1906 – republished by Dover.
11. ^ ^{a b c} Charlot, P.; Jacobs, C. Southward.; Gordon, D.; Lambert, South.; et al. (2020), "The third realization of the International Celestial Reference Frame by very long baseline interferometry", Astronomy and Astrophysics, 644: A159, arXiv:2010.13625, Bibcode:2020A&A...644A.159C, doi:10.1051/0004-6361/202038368, S2CID 225068756
12. ^ ^{a b c d e} MacMillan, D. S.; Fey, A.; Gipson, J. G.; et al. (2019), "Galactocentric acceleration in VLBI analysis", Astronomy and Astrophysics, 630: A93, Bibcode:2019A&A...630A..93M, doi:10.1051/0004-6361/201935379, S2CID 198471325
13. ^ Hagihara, Yusuke (1933), "On the Theory of Secular Aberration", Proceedings of the Physico-Mathematical Society of Japan, 3rd Series, 15 (three–6): 175, doi:x.11429/ppmsj1919.15.3-6_155, the correction of star places with secular aberration is not at all necessary and is fifty-fifty inconvenient, and so long as the solar motion remains uniform and rectilinear.
14. ^ Kovalevsky, J. (2003), "Abnormality in proper motions", Astronomy and Astrophysics, 404 (2): 743–747, Bibcode:2003A&A...404..743K, doi:x.1051/0004-6361:20030560
15. ^ ^{a b c} Titov, O.; Lambert, S. B.; Gontier, A.-Thousand. (2011), "VLBI measurement of the secular abnormality migrate", Astronomy and Astrophysics, 529: A91, arXiv:1009.3698, Bibcode:2011A&A...529A..91T, doi:10.1051/0004-6361/201015718, S2CID 119305429
16. ^ "Gaia's measurement of the solar system acceleration with respect to the distant universe". esa.int. European Space Agency. 3 Dec 2020. Retrieved 14 September 2022.
17. ^ Gaia Collaboration; Klioner, South. A.; et al. (2021), "Gaia Early Data Release iii: Acceleration of the Solar Arrangement from Gaia astrometry", Astronomy & Astrophysics, 649: A9, arXiv:2012.02036, Bibcode:2021A&A...649A...9G, doi:10.1051/0004-6361/202039734
18. ^ ^{a b c d} Eppenstein 1911, p. 54.
19. ^ Bradley, James; Rigaud, Stephen Peter (1832). Miscellaneous works and correspondence of the Rev. James Bradley, D.D., F.R.S. Oxford: University Press. p. eleven.
20. ^ ^{a b} Eppenstein 1911, p. 55.
21. ^ ^{a b} Berry, Arthur (1961) [1898]. A Curt History of Astronomy . Dover. ISBN9780486202105.
22. ^ Hoiberg, Dale H., ed. (2010). "abnormality, constant of". Encyclopædia Britannica. Vol. I: A-ak Bayes (15th ed.). Chicago, IL: Encyclopædia Britannica Inc. pp. xxx. ISBN978-1-59339-837-8.
23. ^ ^{a b} James Bradley (1729). "An account of a new discovered motion of the fixed stars". Philosophical Transactions of the Regal Society. 35: 637–661. doi:ten.1098/rstl.1727.0064.
24. ^ Sakellariadis, Spyros (1982). "Descartes' Experimental Proof of the Space Velocity of Light and Huygens' Rejoinder". Archive for History of Verbal Sciences. 26 (1): i–12. doi:10.1007/BF00348308. ISSN 0003-9519. JSTOR 41133639. S2CID 118187860.
25. ^ Encyclopædia Britannica Archived 2013-11-xi at the Wayback Machine
26. ^ ^{a b c d} Whittaker, Edmund Taylor (1910), A History of the theories of aether and electricity (ane. ed.), Dublin: Longman, Light-green and Co., archived from the original on 2016-02-15
    Whittaker, Edmund Taylor (1953). A History of the Theories of Aether and Electricity (ii. ed.). T. Nelson.
27. ^ Janssen, Michel & Stachel, John (2010), "The Optics and Electrodynamics of Moving Bodies" (PDF), in John Stachel (ed.), Going Critical, Springer, ISBN978-1-4020-1308-9, archived (PDF) from the original on 2022-10-09
28. ^ Darrigol, Olivier (2000), Electrodynamics from Ampére to Einstein , Oxford: Clarendon Printing, ISBN0-19-850594-ix
29. ^ Shankland, R. S. (1963). "Conversations with Albert Einstein". American Journal of Physics. 31 (ane): 47–57. Bibcode:1963AmJPh..31...47S. doi:x.1119/1.1969236.

Farther reading [edit]

• This article incorporates text from a publication at present in the public domain:Eppenstein, Otto (1911). "Aberration". Encyclopædia Britannica. Vol. one (11th ed.). pp. 54–61.
• P. Kenneth Seidelmann (Ed.), Explanatory Supplement to the Astronomical Annual (University Science Books, 1992), 127–135, 700.
• Stephen Peter Rigaud, Miscellaneous Works and Correspondence of the Rev. James Bradley, D.D. F.R.S. (1832).
• Charles Hutton, Mathematical and Philosophical Dictionary (1795).
• H. H. Turner, Astronomical Discovery (1904).
• Thomas Simpson, Essays on Several Curious and Useful Subjects in Speculative and Mix'd Mathematicks (1740).
• de:Baronial Ludwig Busch, Reduction of the Observations Fabricated by Bradley at Kew and Wansted to Make up one's mind the Quantities of Aberration and Nutation (1838).

External links [edit]

• Courtney Seligman on Bradley's observations

Constant Velocity Free Body Diagram,

Source: https://en.wikipedia.org/wiki/Aberration_(astronomy)

Posted by: scottgasked.blogspot.com

Share this post